
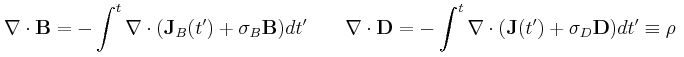
Mode d'emploi de Meep
Paragraphe sur les non-linéarités
Meep résout les équations de Maxwell suivantes par une méthode FDTD (finite-difference in time domain).

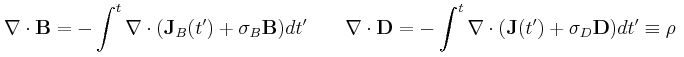
Meep est assez blagueur avec les unités. Dans son système, ε0, μ0 et c valent 1.
L'idée avec Meep est de prendre une longueur caractéristique du problème a, de lui associer un temps caractéristique a/c, les fréquences sont donc en unité de c/a.
La longueur d'onde dans le vide est en unité de a ce qui est cohérent avec c/f où f est en c/a. Si on connaît λ, comme λ = c/f, on a f = c/λ, d'où avec les unités de Meep (on remplace c par 1 et λ par λ/a): f = a/λ
Pour démarrer : ouvrir la console et taper meep
Pour arrêter : taper (exit)
Une fois qu'on a démarré Meep, on peut taper les instructions les unes après les autres comme dans la console Scilab.
Sinon on peut toutes les regrouper dans un fichier .ctl puis lancer le fichier en tapant : meep nom_fichier.ctl >& nom_fichier.out
Les sorties renvoyées lors de l'exécution du programme seront inscrite dans le fichier .out
Pour avoir la coloration syntaxique, utiliser celle de Scheme.
Il faut d'abord indiquer la cellule de calcul. Par exemple pour faire une grille de 16 par 8 sans extension suivant z :
(set! geometry-lattice (make lattice (size 16 8 no-size)))
Ensuite, on donne la géométrie du guide, par exemple un guide 2D horizontal d'épaisseur 1 centré sur l'origine et de permitivité diélectrique 12 :
(set! geometry (list
(make block (center 0 0) (size infinity 1 infinity)
(material (make dielectric (epsilon 12))))))
Attention : l'axe x va vers la droite (normal) mais l'axe y va vers le bas !
Enfin, on ajoute un matériau absorbant (un pml, perfectly matched layers) sur le pourtour de la grille, ici on lui donne une épaisseur de 1 :
(set! pml-layers (list (make pml (thickness 1.0))))
Pour le calcul, Meep discrétise l'espace et le temps. On lui donne le nombre de pixels qui constituent l'unité de longueur, par exemple 10, ce qui donnera une grille de 160 par 80.
(set! resolution 10)
On lance le calcul en indiquant ce qu'on veut que Meep nous trouve, et sur quelle durée il doit faire le calcule, ici, il va calculer jusqu'à 200 (quelle unité de temps ?) et donner la valeur de ε à t =0 et la composante Ez à t=200:
(run-until 200
(at-beginning output-epsilon)
(at-end output-efield-z))
Les résultats sont dans les fichiers nom_fichier-eps-000000.00.h5 et nom_fichier-ez-000200.00.h5. Ces noms indiquent le nom du fichier .ctl à partir duquel le calcul a été fait et le temps auquel correspond le résultat. Les données sont au format h5 et doivent être converties pour être affichées.
Pour convertir en .png, par exemple :
h5topng -S3 nom_fichier-eps-000000.00.h5
-S3 augmente la taille (scale) par 3.
Ceci affiche le ε, pour avoir le champ Ez :
h5topng -S3 -Zc dkbluered -a yarg -A nom_fichier-eps-000000.00.h5 nom_fichier-ez-000200.00.h5
-Zc dkbluered code les valeurs en échelles de bleu et rouge.
-a yarg -A superpose le premier fichier (le ε) au deuxième en gris.
Au lieu de remplir les paramètres des différents guides et sources avec des valeurs numériques, on peut commencer par définir les variables nécessaires contenant les-dites valeurs numériques puis y faire appel dans les fonctions.
En vue de définir un anneau
(define-param n 3.4) ; index of waveguide
(define-param w 1) ; width of waveguide
(define-param r 1) ; inner radius of ring
(define-param pad 4) ; padding between waveguide and edge of PML
(define-param dpml 2) ; thickness of PML
(define sxy (* 2 (+ r w pad dpml))) ; cell size
Si on veut, par la suite, lancer une modélisation avec d'autres valeurs de paramètres, il n'y a pas besoin d'éditer le fichier .ctl, il suffit de donner la valeur du paramètre en lançant meep, par exemple si on veut une épaisseur de guide de 2 au lieu de 1 :meep w=2 fichier.ctl
Pour faire une partie d'un script si une condition est vérifiée, on utilise (if condition (instructions si vraie) (instructions si faux)).
Règle
(set! geometry (list
(make block (center 0 0) (size infinity 1 infinity)
(material (make dielectric (epsilon 12))))))
Coude à angle droit
(set! geometry (list
(make block (center -2 -3.5) (size 12 1 infinity)
(material (make dielectric (epsilon 12))))
(make block (center 3.5 2) (size 1 12 infinity)
(material (make dielectric (epsilon 12))))))
Anneau (on fait deux cylindres coaxiaux, le deuxième vidant le premier)
(set! geometry (list
(make cylinder (center 0 0) (height infinity)
(radius (+ r w)) (material (make dielectric (index n))))
(make cylinder (center 0 0) (height infinity)
(radius r) (material air))))
Démarrage brutal à t=0
(set! sources (list
(make source
(src (make continuous-src (frequency 0.15)))
(component Ez)
(center -7 0))))
Démarrage en tanh de durée caractéristique 20 unités de temps
(set! sources (list
(make source
(src (make continuous-src
(wavelength (* 2 (sqrt 12))) (width 20)))
(component Ez)
(center -7 -3.5) (size 0 1))))
Spectre gaussien
(define-param fcen 0.15) ; pulse center frequency
(define-param df 0.1) ; pulse width (in frequency)
(set! sources (list
(make source
(src (make gaussian-src (frequency fcen) (fwidth df)))
(component Ez) (center (+ r 0.1) 0))))
Il faut d'abord calculer la composante du champ à différents instants au lieu de simplement à la fin (on va donc remplacer le at-end par un at-every):
(run-until 200
(at-beginning output-epsilon)
(to-appended "ez" (at-every 0.6 output-efield-z)))
Ceci va créer le fichier ez.h5 si on est en ligne de commande ou le fichier Nom_Fichier-ez.h5 si on lance le fichier de commmande Nom_Fichier.ctl.
On peut vérifier que les calculs se sont bien passé en lançant la commande suivante dans la console (pas dans la console Meep !):
h5ls ez.h5
La réponse est :
ez Dataset {161, 161, 330/Inf}
qui indique que le fichier ez.h5 contient un tableau de 162 × 162 × 330, la dernière dimension étant le temps.
On peut choisir de sortir une image à partir de n'importe quel instant avec la commande h5topng en ajoutant l'option -t 229 (qui sort l'image à la date 229) mais, pour faire une animation, il faut créer une image pour chaque instant :
h5topng -t 0:329 -R -Zc dkbluered -a yarg -A eps-000000.00.h5 ez.h5
l'option -R donne un choix d'échelle de bleu-rouge commune à toutes les images.
Maintenant que toutes les images sont préparées, il faut les réunir pour faire une animation (on utilise ImageMagick):
convert ez.t*.png ez.gif
On peut remplacer .gif par .mpg pour sortir une animation Mpeg au lieu de gif.
Si on veut juste sortir une animation, comme précédemment, on n'est pas obligé de faire tout calculer, on a juste besoin d'images, stockées plus efficacement que sous forme de tableau de nombres. Au lieu de taper la commande output-efiel-z on tape output-png Ez "-Zc dkbluered" qui va créer un fichier png tous les 0.6 unités de temps qui peuvent ensuite être assemblés en animation comme précédemment.
Un inconvénient quand même : l'échelle des couleurs n'est plus commune à toutes les images, il manque ce qu'on faisait avec l'option -R.
Pour éviter que les fichiers images n'encombrent le dossier de travail, on peut demander à créer un sous-dossier pour les loger avec la commande (use-output-directory) à placer avant le run-until. Les images (et tous les autres fichiers calculés .h5, .png...) seront enregistrées dans le sous-dossier Nom_fichier-out si le fichier de commande est Nom_fichier.ctl.
On peut calculer le spectre de transmission et/ou réflexion d'une structure (comme une cavité résonante) en réponse à une excitation.
La première idée est de calculer la réponse de la structure pour chaque pulsation séparément mais le plus efficace est de faire la transformée de Fourier de la réponse à une excitation très courte. Un pulse d'excitation correspond à un large spectre dans l'espace des pulsations donc si on regarde la réponse de la structure après transmission dans l'espace des pulsations, on a la réponse pour un large spectre, ie. le spectre de transmission de la structure.
La puissance transmise à une ω par la strucuture est donnée par le flux du vecteur de Poynting Π(ω) = Re(Intégrale (Eω(x)* × Hω(x) d2x))
Pour avoir le flux du vecteur de Poynting dans l'espace des ω, il ne faut pas faire la TF du flux du vecteur de Poynting dans l'espace des temps.
(Ce qui semble facile à faire : Meep donne E et H à chaque instant, on fait le produit vectoriel à chaque instant pour avoir Π(t) puis on calule le flux puis on fait la TF.)
Il faut faire la TF des champs E et H puis calculer leur produits vectoriel. En effet, la TF du flux n'est pas le flux de la TF.
Maintenant, comment faire la TF des champs E et H puisque Meep calcule E(t) et H(t) ?
La TF est donnée par : E(ω) = 1/sqrt(2 π) intégrale (E(t) exp(i ω t) dt)
qu'on peut approximer en remplaçant les intégrales par des sommes discrètes
E(ω) = 1/sqrt(2 π) sommen E(n Δt) exp(i ω n Δt) Δt
Ensuite, quand on connaît le flux du vecteur de Poynting, il faut calculer le coefficient de transmission en le comparant au flux incident. Pour cela, on lance Meep deux fois : une fois sans la structure puis une fois avec la structure en normalisant cette deuxième réponse à l'aide de la première.
Voir l'exemple dans Meep/Essais/transmission spectrum/ bend-flux.ctl. On y calcule la transmission, la réflexion et les pertes dans un coude.
Le début du script permet de préparer la géométrie. Pour calculer la transmitance on normalise le flux après passage du coude par rapport au flux qu'on obtient après passage dans un guide droit. Il faut donc calculer le flux pour les deux géométries : droit et coude. Cela se fait avec un seul script mais une définition de géométrie avec un if.
La source utilisée est un pulse gaussien dans le domaine des fréquences de largeur df=0.1 autour de fcen=0.15. On donne sa taille et sa position.
On ajoute un pml.
On calcule les flux, il faut le faire après avoir spécifié la géomatrie, les sources, la résolution etc. car les paramètres des champs sont réinitialisés quand on crée des plans au travers desquels on calcule les flux. Il faut indiquer où se fait le calcul et pour quelles fréquences. Dans l'exemple, les flux sont calculés pour nfreq fréquences différentes, centrées autour de fcen et séparée les unes des autres de df.
calcul des flux transmis et réfléchi
(define trans ; flux transmis
(add-flux fcen df nfreq
(if no-bend?
(make flux-region
(center (- (/ sx 2) 1.5) wvg-ycen) (size 0 (* w 2) 0)) ;apparemment le dernier 0 pas indispensable
(make flux-region
(center wvg-xcen (- (/ sy 2) 1.5)) (size (* w 2) 0) )
)))
(define refl ; flux réfléchi
(add-flux fcen df nfreq
(make flux-region
(center (+ (* -0.5 sx) 1.5) wvg-ycen) (size 0 (* w 2))
)))
Pour calculer le spectre de réflexion, il faut comparer le flux réfléchi et le flux incident. Le problème c'est qu'il n'est pas simple de calculer le flux réfléchi car le champ réfléchi est superposé au champ incident. Il faut lancer la simulation une fois sans la structure, enregistrer la transformée de Fourier du champ puis relancer la simulation avec la structure en retranchant la transformée de Fourier des champs incidents. On fait cela avec (save-flux "refl-flux" refl) qui enregistre la transformée de Fourier du champ sans le coude puis avec (load-minus-flux "refl-flux" refl) qui charge en ajoutant un moins, la TF enregistrée avant et va donc la retrancher à la TF calculée avec le coude.
On demande d'afficher les flux. Pour pouvoir se servir des résultats par la suite, il faut que cet affichage soit dirigé vers un fichier de sauvegarde, ce qui se fait au moment de lancer meep avec l'instruction tee: meep no-bend?=true bend-flux.ctl | tee bend0.out.
L'ennui c'est qu'on a récupéré tout ce qui est affiché pendant le déroulement de meep, les premières lignes sont encombrantes, il faut s'en débarrasser avec grep flux1: bend0.out > bend0.dat
On peut ensuite tracer les spectres dans Scilab avec csvRead("bend0.dat") au lieu de fscanfMat car c'est un fichier texte UTF-8 à ouvrir.
On excite la structure avec un pulse court en plaçant la source dans la structure puis quand la source est coupée, on analyse les champs qui rebondissent dans la structure pour avoir leur pulsation et leur temps de décroissance.
La première idée pour faire cette analyse est de regarder l'évolution dans la temps du champ et d'en faire la TF, les modes propres donnent des pics dans le spectre. Le problème c'est qu'il faut faire des calculs sur des temps longs pour avoir une bonne résolution en fréquence et "the problem of extracting the decay rates leads to a poorly-conditioned nonlinear fitting problem."
Au lieu de ça, Meep permet de faire un traitement du signal plus rafiné emprunté à la spectroscopy RMN, l'algorithme est appelé filter diagonalization et est implémenté dans le paquet Harminv. Harminv isole toutes les fréquences, leurs amplitudes et leur taux de décroissance en un temps assez court. Un temps de vie de 109 périodes peut être trouvé avec une durée d'acquisition de seulement quelques centaines de périodes.
Quand on a les fréquences des modes, si on veut le motif du champ, il faut relancer la simulation avec une bande de fréquence étroite (donc une excitation longue) autour de la fréquence du mode en question
Voir l'exemple dans Meep/Essais/Anneau/anneau.ctl
La source est gaussienne dans le domaine des fréquences.
(define-param fcen 0.15) ; pulse center frequency
(define-param df 0.1) ; pulse width (in frequency)
(set! sources (list
(make source
(src (make gaussian-src (frequency fcen) (fwidth df)))
(component Ez) (center (+ r 0.1) 0))))
Il faut faire tourner la simulation pendant le temps de fonctionnement de la source et attendre encore un certain temps pendant lequel on va faire l'analyse des champs avec harminv pour identifier les fréquences et les taux de décroissance des modes excités.
(run-sources+ 300
(at-beginning output-epsilon)
(after-sources (harminv Ez (vector3 (+ r 0.1)) fcen df)))
La syntaxe de la fonction est :harminv champ position fréquence centrale largeur de bande de fréquences à analyser.
Dans l'exemple précédent, harminv est mise dans after-sources pour analyser les fréquences dans le système débarrasé des sources.
Le résultat de harminv s'affiche dans la console après harminv0: ce qui permet de choper le résultat avec grep. Les 6 colonnes de résultats ont la signification suivantes :
Pour une meilleure précision, on peut relancer la simulation en rétrécissant la bande de fréquence de la source autour d'une des fréquences trouvées avec harminv. Cela débarrase le système des plein de champs et donne de meilleurs résultats.
meep fcen=0.118 df=0.01 fichier.ctl
Une fois qu'on a un mode, on veut le visualiser, pour cela, on ajoute la ligne qui suit à la fin du script. On n'ajoute pas at-end output-efield-z dans le run-sources+ car, quand la source s'éteind, on peut être dans un moment où le champ Ez est nul (toute l'énergie est dans H). le run-until permet de calculer 20 champs Ez sur une période 1/fcen.
Une fois la ligne ajoutée, on relance meep.
(run-until (/ 1 fcen)(at-every(/ 1 fcen 20) output-efield-z))
Il faut ensuite convertir les résultats en images et les assembler en film :
h5topng -RZc dkbluered -C eps-0000.h5 fichier-ez-*.h5
convert fichier-ez-*.png fichier.gif
| Option | Fonction |
|---|---|
| -Sn | Applique une échelle égale à n |
| -Z | Centre l'échelle de couleur autour de zéro |
| -R | Utilise le min et le max de l'ensemble des fichiers .h5 pour caler l'échelle de couleur |
| -c bluered | Utilise l'échelle de teinte bluered
|
| -o file | Enregistre le fichier .png avec le nom file.png au lieu d'utiliser le nom du fichier .h5 |
| -C file | Superpose le contour du fichier file sur les images |
| -A file -a colormap:opacity | Superpose le fichier file aux autres fichiers
en lui donnant une opacité (entre 0 et 1, 0 : complètement transparent) Les échelles de teintes colormap qui donnent bien : yellow, gray, yarg, green, bluered |
| Instruction | signification |
|---|---|
| convert file.gif -resize nxn resize_file.gif | Agrandit ou réduit l'image pour qu'elle entre dans un carré de côté n mais en gardant ses proportions. |
| convert file.gif -resize nxn\! resize_file.gif | Agrandit ou réduit l'image et la déforme pour qu'elle occupe exactement le carré de côté n mais en gardant ses proportions. |
| convert file.gif -resize n% resize_file.gif | Agrandit ou réduit l'image d'un facteur n% en gardant ses proportions. |